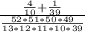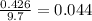Question

A bridge hand is made up of 13 cards from a deck of 52. find the probability that a hand chosen at random contains at least 3 kings kings.

Answer 1

1.
In total there are C(52, 13) ways that we can pick a hand, that is
`(52!)/(13!39!)`


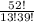
2.
P(a hand contains at least 3 kings)
=P(a hand contains exactly 3 kings)+P(a hand contains 4 kings)

3.
first let's find P(a hand contains exactly 3 kings):

P(a hand contains exactly 3 kings)
=n(a hand contains exactly 3 kings)/C(52, 13)

n(a hand contains exactly 3 kings)=C(4, 3)*C(48, 10)

where C(4,3) is the total number of ways we can pick 3 out of 4 kings,

C(48, 10) is the number of picking 10 letters to complete a hand, out of the 52-4=48 non-king cards.

so P(a hand contains exactly 3 kings)=[C(4, 3)*C(48, 10)]/C(52, 13)

4. with the same reasoning as in step 3:

P(a hand contains 4 kings)=n(a hand contains 4 kings)/C(52, 13)

= [C(4, 4)*C(48, 9]/C(52, 13)


5.

P(a hand contains at least 3 kings)
=P(a hand contains exactly 3 kings)+P(a hand contains 4 kings)

=[C(4, 3)*C(48, 10)]/C(52, 13)+ [C(4, 4)*C(48, 9)]/C(52, 13)

=
`(C(4, 3)*C(48, 10)+C(4, 4)*C(48, 9))/(C(52, 13))`

=
`(4* (48!)/(10!38!) + (48!)/(9!39!))/( (52!)/(13!39!) )`

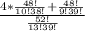
simplify by 38! in the denominators and 48! in the numerators :


`(4* (1)/(10!) + (1)/(9!39))/( (52*51*50*49)/(13!39) )`

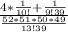
now simplify by 9! in all denominators:


`( (4)/(10)+ (1)/(39) )/( (52*51*50*49)/(13*12*11*10*39))`



`( 0.426 )/( 9.7) =0.044`