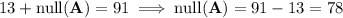Question

The matrix a is 13 by 91. give the smallest possible dimension for nul

a.

Answer 1

Use the rank-nullity theorem. It says that the rank of a matrix
`\mathbf A`,
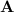
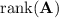
`\mathrm{rank}(\mathbf A)`, has the following relationship with its nullity
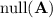
`\mathrm{null}(\mathbf A)` and its number of columns
`n`:


`\mathrm{rank}(\mathbf A)+\mathrm{null}(\mathbf A)=n`

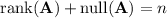
We're given that
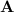
`\mathbf A` is
`13*91`, i.e. has
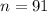
`n=91` columns. The largest rank that a
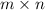
`m* n` matrix can have is
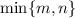
`\min\{m,n\}`; in this case, that would be 13.

So if we take
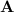
`\mathbf A` to be of rank 13, i.e. we maximize its rank, we must simultaneously be minimizing its nullity, so that the smallest possible value for
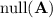
`\mathrm{null}(\mathbf A)` is given by


`13+\mathrm{null}(\mathbf A)=91\implies\mathrm{null}(\mathbf A)=91-13=78`