Question

What is the sum of the first five terms of a geometric series with a1 = 10 and r = 1/5?

Answer 1

a₁ = 10
r = 1/5

Sum of GP = a₁(1-rⁿ)/(1-r), where a₁ = 1st term; n= rank and r = common ratio

Sum = 10[1-(1/5)⁵] /(1-1/5)
Sum = 10(1-1/3250)/(4/5)
Sum = 1562/125

Answer 2

Answer: 12.496

Explanation:

The formula to find the sum of geometric progression is given by :-

`S_n=(a(1-r^n))/(1-r)`

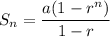
Given : The first term :
`a_1=10`

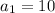
Common ratio =
`r=(1)/(5)=0.2`

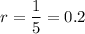
Then , the sum of first five terms of a geometric series is given by :-

`S_5=(10(1-(0.2)^5))/(1-0.2)=12.496`

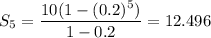
Hence, the sum of the first five terms of given geometric series =12.496