Question

99 points ALGERBA 1 HELLP

Given the function h(x) = 3(2)x, Section A is from x = 1 to x = 2 and Section B is from x = 3 to x = 4.

Part A: Find the average rate of change of each section.

Part B: How many times greater is the average rate of change of Section B than Section A? Explain why one rate of change is greater than the other.

Answer 1

PART A

The given equation is
`3(2)^(x)`

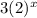
When
`x=1`,
`h(1)=3 (2)^(1)=6`
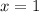
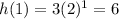
When
`x=2`,
`h(2)=3 (2)^(2)= 12`
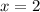
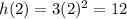
When
`x=3`,
`h(3)=3 (2)^(3) = 24`
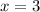
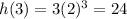
When
`x=4`,
`h(4)=3 (2)^(4)=48`

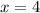
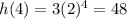
Between
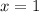
`x=1` and
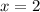
`x=2` there is an increase by 12
Between
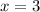
`x=3` and
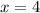
`x=4` there is an increase by 24

PART B

The change in section B is twice the change in section A. This change is an exponential change indicated by the expression
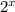
`2^(x)` in the function. If we continue to check the rate of change between
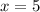
`x=5` and
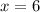
`x=6`, we will discover that the change will be four times the rate of change between
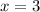
`x=3` and
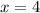
`x=4`.