Question

Please check answer!

Use graphs and tables to find the limit and identify any vertical asymptotes of limit of 1 divided by the quantity x minus 3 as x approaches 3 from the left

∞; x = -3
-∞; x = -3
-∞; x = 3
1 ; no vertical asymptotes

Is it A?

Answer 1

the function is
`f(x)= (1)/(x-3)`

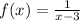
we are looking at
`\lim_(x \to \ 3^(-) ) (1)/(x-3)`, that is, we are looking at what happens with the function when x are values very very close to 3, from the left.

method 1: using tables


`\lim_(x \to \ 3^(-) ) (1)/(x-3)` is approximately the value of f at a number very very close to 3, but a little less than 3.

this number can be thought as a=2.9999999998

a-3 is negative,since a is very close to 3, but smaller.


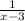
`(1)/(x-3)` for x=a is
`(1)/(0.0000000002) =20000000000`

so for values of x closer to 3,
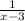
`(1)/(x-3)` is larger and larger, in the negative direction.

This means that
`\lim_(x \to \ 3^(-) ) (1)/(x-3)`=-∞ and the asymptote is the vertical line x=3, since for x=3, the function is not defined.

method 2: by graphing the function using a graphic calculator, we see that the graph gets very very close to the vertical line x=3, but never touches it, so this line is a vertical asymptote.

Also, we see that the closer x gets to 3, the smaller the value of f becomes, so


`\lim_(x \to \ 3^(-) ) (1)/(x-3)`=-∞


Answer:

-∞; x = 3