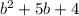Question

The volume of a rectangular prism is b3 + 8b2 + 19b + 12 cubic units, and its height is b + 3 units. The area of the base of the rectangular prism is square units.

Answer 1

b^2 + 5b +4

Explanation:

Answer 2

Given:

The volume of the rectangular prism is


`b^(3)+8 b^(2) +19b+12`,

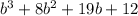
the height is h=(b+3)

1. The volume of a rectangular prism is (base area)*height

also, notice that the volume is a third degree polynomial, the height is a 1st degree polynomial, so the base area must be a 2nd degree polynomial, whose coefficients we don't know yet.
Let this quadratic polynomial be
`(mb^(2)+nb+k)`


2


`b^(3)+8 b^(2) +19b+12=(mb^(2)+nb+k)*(b+3)`


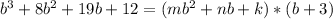
notice that
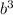
`b^(3)` is the product of the largest 2 terms:
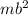
`mb^(2)` and b, so m must be 1

also, notice that 12 is the product of the constants, k and 3

so k*3=12, this means k=4

3
we write the above equality again:


`b^(3)+8 b^(2) +19b+12=(b^(2)+nb+4)*(b+3)`



`(b^(2)+nb+4)(b+3)= b^(3)+3 b^(2) +nb^(2)+3nb+4b+12`

=
`= b^(3)+(n+3)b^(2)+(3n+4)b+12`


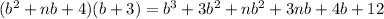
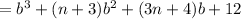
4
now compare the coefficient with the left side:


`8 b^(2)=(n+3)b^(2)`

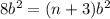
8=n+3

n=5


substituting n=5:

the base area is
`b^(2)+5b+4`

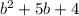
Answer:
`b^(2)+5b+4`