Question

BC is tangent to circle A at B and to circle D at C. What is AD to the nearest tenth? Look at image attached.

Answer 1

1. 19.2

Step-by-step explanation:

Please find the attachment.

Since we know that radius is perpendicular to tangent of a circle. So AB will be perpendicular to BC at c and DC is perpendicular to CB at C.

Now we will construct a perpendicular line to radius AB at point E from the center of our small circle. Since we have two right angles at point B and C so we will also have right angles at point E and D as well.

Length of CD is is 7 so length of BE will be 7 as well and length of EA will be 10-7=3. Length of DE will be equal to length BC that is 19.

Now we have formed a right triangle and now we will use Pythagoras theorem to find the length of AD.

`(AD)^(2)=(DE)^(2)+(EA)^(2)`

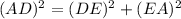
Upon substituting our values in above formula we will get,

`(AD)^(2)=(19)^(2)+(3)^(2)`

`(AD)^(2)=361+9`

`(AD)^(2)=370`

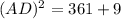
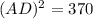
Upon taking square root of both sides of our equation we will get,

`AD=√(370)`

`AD=19.2353840616713448\approx 19.2`

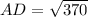
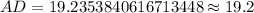
Therefore, the length of AD will be 19.2 and 1st option is the correct choice.

Answer 2

A tangent line to a circle is perpendicular to the radius drawn to the tangent point ⇒
AB ⊥ BC and CD ⊥ BC ⇒ ABCD is a right trapezoid.

You can find the AD using formula:


`AD= √(BC^2+(AB-CD)^2) \\ \\ AD= √(19^2+(10-7)^2) = √(361+9)= √(370) \approx 19.2`