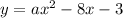
1.
the line of symmetry is x=2, means that the x coordinate of the vertex is x=2.
the point x=2 is the midpoint of the roots
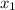
and
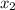
.
so
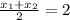
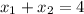
Remark: in the x-axis, if c is the midpoint of a and b, then
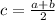
2.
since
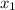
and
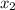
are roots
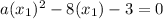
and
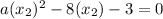
3.
equalizing:
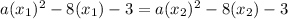
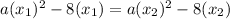

in the left side factorize a, in the left side factorize 8:
![a[(x_1)^(2)-(x_2)^(2)] =8(x_1 -x_2)](https://img.qammunity.org/2018/formulas/mathematics/college/gmcd6varirvbdfnpvu9ats13x7kksq4zz1.png)
in the right side use the difference of squares formula:
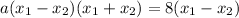
simplify by
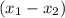
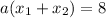
substitute
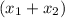
with 4:
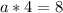
a=2
Answer: C)2