Question

Given f(x), use Remainder Theorem to find f(4). f (x) = 2x^3 – 11x^2 + 7x - 5

Answer 1

`f(x)=2x^3-11x^2+7x-5`

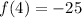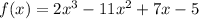
To find f(4) you divide the given polynomial into (x-4):

To divide:

1. Divide the first term of the dividend by the highest term of the divisor:

`(2x^3)/(x)=2x^2`

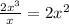
2. Multiply the divisor by the result:

`2x^2(x-4)=2x^3-8x^2`

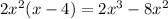
3. Substract the product in step 2 from the appropiat terms of the dividend (when you substract the symbols change) (then bring down the next term from the dividend)

4. Repeat previous steps:

`(-3x^2)/(x)=-3x`
`-3x(x-4)=-3x^2+12x`
`(-5x)/(x)=-5`
`-5(x-4)=-5x+20`

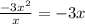
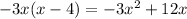
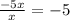
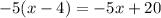
As the remainder is -25:

`f(4)=-25`