Question

(05.01 MC)

The table and the graph below each show a different relationship between the same two variables, x and y:

How much more would the value of y be on the graph than its value in the table when x = 12?
20
30
60
70

Answer 1

The correct option is C. The value of y be on the graph than is 60 more than the y value in the table when x = 12.

Explanation:

If a line passing through two points then the equation of line is

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

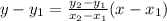
From the given table it is clear that the line passing thought the points (4,100) and (5,125).

`y-100=(125-100)/(5-4)(x-4)`

`y-100=25(x-4)`

`y-100=25x-100`

`y=25x`

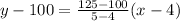
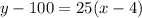
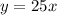
The value of this function at x=12 is

`y=25(12)=300`

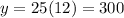
From the given table it is clear that the line passing thought the points (0,0) and (2,60).

`y-0=(60-0)/(2-0)(x-0)`

`y=30x`

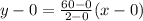
The value of this function at x=12 is

`y=30(12)=360`

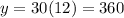
The difference between y value in the graph and in the table at x=12 is

`360-300=60`

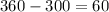
The value of y be on the graph than is 60 more than the y value in the table when x = 12. Therefore the correct option is C.

Answer 2

For the table, y = 25x.
When x = 12, y = 25*12 = 300

For the graph, y = 30x
When x = 12, y = 30*12 = 360

When x = 12, the value of y on the graph is 60 more than its value in the table.