Question

In physics, if a moving object has a starting position at s 0, an initial velocity of v 0, and a constant acceleration a, then the position S at any time t > 0 is given by:

S = at 2 + v 0 t + s 0.

Solve for the acceleration, a, in terms of the other variables. For this assessment item, you can use ^ to show exponents and type your answer in the answer box, or you may choose to write your answer on paper and upload it.

Answer 1

Actually the position function with respect to time under constant acceleration is:

a=g

v=⌠g dt

v=gt+vi

s=⌠v

s=gt^2/2+vit+si

So if vi and si are zero then you just have:

s=gt^2/2

Notice that it is not gt^2 but (g/2) t^2

So the first term in any quadratic is half of the acceleration times time squared because of how the integration works out...

Anyway....

sf=(a/2)t^2+vit+si

(sf-si)-vit=a(t^2)/2

2(sf-si)-2vit=at^2

a=(2(sf-si)-2vit)/t^2 and if si and vi equal zero

a=(2s)/t^2

Answer 2

Explanation:

The equation of a moving object in physics is given by :

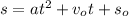`s=at^2+v_ot+s_o`...........(1)

Where

s₀ is the starting position of an object

a is the acceleration of the object

v₀ is the initial velocity of the object

t is the time taken

We need to find the value of acceleration by rearranging equation (1). Subtract
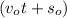`(v_ot+s_o)` on both sides of equation (1) as :

`s-v_ot-s_o=at^2`

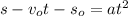
Divide both sides of above equation by t² as :

`a=(s-v_ot-s_o)/(t^2)`

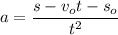
So, the value of acceleration is
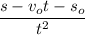`(s-v_ot-s_o)/(t^2)`. Hence, this is the required solution.