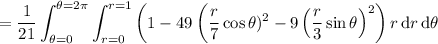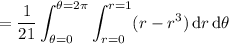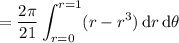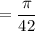Question

greens theorem. find the max value of the line integral where f=(13x^2y+3y^3-y)i-12x^3j and C is any positively oriented closed curve. max=?

Answer 1

The line integral is given by


`\displaystyle\int_C\mathbf f\cdot\mathrm d\mathbf r=\int_C((13x^2y+3y^3-y)\,\mathrm dx-12x^3\,\mathrm dy)`

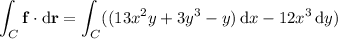
By Green's theorem, the line integral along
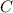
`C` is equivalent to the double integral over
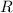
`R` (the region bounded by
`C`)


`\displaystyle\iint_R\left((\partial(-12x^3))/(\partial x)-(\partial(13x^2y+3y^3-y))/(\partial y)\right)\,\mathrm dx\,\mathrm dy`

`=\displaystyle\iint_R(-36x^2-(13x^2+9y^2-1))\,\mathrm dx\,\mathrm dy`

`=\displaystyle\iint_R(1-49x^2-9y^2)\,\mathrm dx\,\mathrm dy`

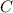
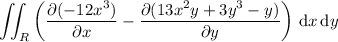
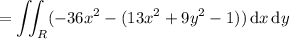
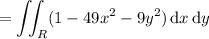
Now consider the function
`g(x,y)=1-49x^2-9y^2`. We can think of the double integral above as a volume integral; namely, it's the volume of the region below
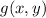
`g(x,y)` and above the region
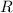
`R` in the
`x`-
`y` plane (i.e.
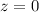
`z=0`). This volume will be maximized if
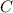
`C` is taken to be the intersection of
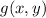
`g(x,y)` with the plane, which means
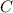
`C` is the ellipse
`49x^2+9y^2=1`.

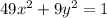
For the double integral, we can convert to an augmented system of polar coordinates using


`\begin{cases}x=\frac17r\cos\theta\\\\y=\frac13r\sin\theta\end{cases}`

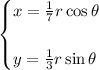
where
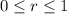
`0\le r\le1` and
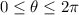
`0\le\theta\le2\pi`. We have the Jacobian determinant


`\det\mathbf J=\left|(\partial(x,y))/(\partial(r,\theta))\right|=\begin{vmatrix}(\partial x)/(\partial r)&(\partial x)/(\partial\theta)\\\\(\partial y)/(\partial r)&(\partial y)/(\partial\theta)\end{vmatrix}`

`\det\mathbf J=\begin{vmatrix}\frac17\cos\theta&-\frac17r\sin\theta\\\\\frac13\sin\theta&\frac3r\cos\theta\end{vmatrix}=\frac r{21}`

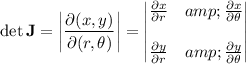
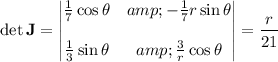
So the double integral, upon converting to our polar coordinates, is equivalent to


`=\displaystyle\frac1{21}\int_(\theta=0)^(\theta=2\pi)\int_(r=0)^(r=1)\left(1-49\left(\frac r7\cos\theta)^2-9\left(\frac r3\sin\theta\right)^2\right)r\,\mathrm dr\,\mathrm d\theta`

`=\displaystyle\frac1{21}\int_(\theta=0)^(\theta=2\pi)\int_(r=0)^(r=1)(1-r^2\cos^2\theta-r^2\sin^2\theta)r\,\mathrm dr\,\mathrm d\theta`

`=\displaystyle\frac1{21}\int_(\theta=0)^(\theta=2\pi)\int_(r=0)^(r=1)(r-r^3)\,\mathrm dr\,\mathrm d\theta`

`=\displaystyle(2\pi)/(21)\int_(r=0)^(r=1)(r-r^3)\,\mathrm dr\,\mathrm d\theta`

`=\frac\pi{42}`