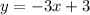to make a perpendicular function from another we must take its slope and make two transformations
the slope of y=1/3x is 1/3
the transformations:
1.
reverse the number
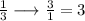
2.
and change the sign
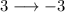
ok we have the slope now need the general equation of the line
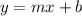
where m is the slope , b a cut point and (x,y) a point
so, we have the slope=-3 , and the point (2,-3) we can replace to find b
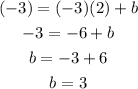
now we can replace b and the slope to have the final equation