Question

The temperature of a mixture changes by -5.2 Fahrenheit between 8am and 11am. At 6pm the temperature is 14.5 Fahrenheit, which is half of what it was at 11am. What was the temperature at 8am of the mixture. I have this equation , but not sure is correct. 1/2(x-6.8)= -3.1

Answer 1

Step-by-step explanation

Let us have a sketch of the question

If the temperature at 6 pm is 14.5 F

And the temperature at 11am is twice that of 6pm

Then the temperature at 11am will be

`2*14.5F=29F`

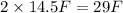
Since the temperature of a mixture changes by -5.2 Fahrenheit between 8 am and 11 am.

Then the temperature at 8 am will be

`\begin{gathered} \theta_(11am)-\theta_(8am)=-5.2 \\ 29F-\theta_(8am)=-5.2F \\ \theta_(8am)=29F+5.2F \\ \theta_(8am)=34.2F \end{gathered}`

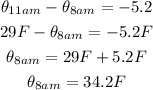
Therefore, the temperature at 8 am will be 34.2 F