Question

How can I do this with the function (x+2)/x-3

Create a rational function with a linear binomial in both the numerator and denominator.
Part 1. Graph your function using technology. Include the horizontal and vertical asymptotes and the x- and y-intercepts on your graph. Label the asymptotes and intercepts.
Part 2. Show all work to identify the vertical asymptote, the x-intercepts, and the y-intercept.

Answer 1

The given rational function is

`f(x) = (x+2)/(x-3)`

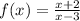
Part 1
The horizontal asymptote is obtained by either long division or synthetic division. It may be obtained also as

`f(x)= (x-3+5)/(x-3) = (x-3)/(x-3) + (5)/(x-3) =1+ (5)/(x-3)`
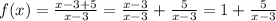
Therefore the horizontal asymptote is
y = 1.

The vertical asymptote occurs when the denominator is zero because the function becomes undefined. Set x-3 = 0 to obtain
x = 3.
Therefore a vertical asymptote occurs at x = 3.

The x-intercept occurs when f(x) = y = 0. Set f(x)=0 to obtain

`(x+2)/(x-3) =0`
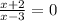
For x≠3, obtain
x+2=0 => x = -2
The x-intercept is x = -2.

The y-intercept occurs when x=0. Set x=0 in f(x) to obtain

`f(0)= (0+2)/(0-3) =- (2)/(3)`
The y-intercept is
y = -2/3

Part 2
The graph of the function is shown below. It identifies the horizontal and vertical asymptotes, the x-intercept, and the y-intercept.