Question

What are the solutions of the equation x6 + 6x3 + 5 = 0? Use factoring to solve.

Answer 1

Consider the equation
`x^6+6x^3+5=0`.

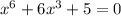First, you can use the substitution
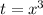`t=x^3`, then
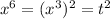`x^6=(x^3)^2=t^2` and equation becomes
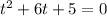`t^2+6t+5=0`. This equation is quadratic, so

`D=6^2-4\cdot 5\cdot 1=36-20=16=4^2,\ √(D)=4,\\ \\ t_(1,2)=(-6\pm 4)/(2) =-5,-1`.

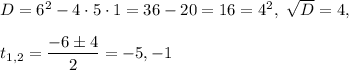Then you can factor this equation:

`(t+5)(t+1)=0`.

Use the made substitution again:

`(x^3+5)(x^3+1)=0`.

You have in each brackets the expression like
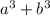`a^3+b^3` that is equal to
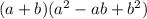`(a+b)(a^2-ab+b^2)`. Thus,

`x^3+5=(x+\sqrt[3]{5})(x^2-\sqrt[3]{5}x+\sqrt[3]{25}) ,\\x^3+1=(x+1)(x^2-x+1)`

and the equation is

`(x+\sqrt[3]{5})(x^2-\sqrt[3]{5}x+\sqrt[3]{25})(x+1)(x^2-x+1)=0`.

Here
`x_1=-\sqrt[3]{5} , x_2=-1` and you can sheck whether quadratic trinomials have real roots:

1.
`D_1=(-\sqrt[3]{5}) ^2-4\cdot \sqrt[3]{25}=\sqrt[3]{25} -4\sqrt[3]{25} =-3\sqrt[3]{25} <0`.

2.
`D_2=(-1)^2-4\cdot 1=1-4=-3<0`.

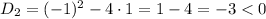This means that quadratic trinomials don't have real roots.

Answer:
`x_1=-\sqrt[3]{5} , x_2=-1`

If you need complex roots, then

`x_(3,4)=\frac{\sqrt[3]{5}\pm i\sqrt{3\sqrt[3]{25}}}{2} ,\\ \\x_(5,6)=(1\pm i√(3))/(2)`.