Question

What statement correctly describes the key features of the graph of f(x) = 4(1/2)^(x + 1 )− 3

Y-intercept of (0, −1), starts up on the left, gets closer to y = −3 on the right

Y-intercept of (0, −1), starts down on the left, gets closer to y = −3 on the right

Y-intercept of (0, 1), starts up on the left, gets closer to y = −3 on the right

Y-intercept of (0, 1), starts down on the left, gets closer to y = −3 on the right

Answer 1

Y-intercept of (0, −1), starts up on the left, gets closer to y = −3 on the right.

You have to plot the graph to see it. Google online graphing calculator and enter the equation.

Answer 2

The correct option is:

"Y-intercept of (0, −1), starts down on the left, gets closer to y = −3 on the right"

Step-by-step explanation:

You have the following function:

`f(x)=y=4*((1)/(2)) ^(x+1) -3`

The intersection on the "y" axis implies that the value at "x" must be zero. So, to calculate the value in "y" you must replace "x" with the value 0 and perform the corresponding calculations:

`y=4*((1)/(2)) ^(0+1) -3`

`y=4*((1)/(2)) -3`

`y=2 -3`

`y=-1`

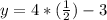
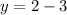
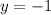
Being (x, y) a point on the graph, the y- intercept is (0,-1).

This function is an exponential function function, whose form corresponds to the general expression:

`g(x)=k*a^(x-h) +b`

Where:

• If a is greater than 1 (a> 1), the function is increasing. On the other hand, if a is less than 1 (a <1), the function is decreasing.

• b is the independent term of the equation and determines the Horizontal Asymptote, which is a horizontal line to which the function is approaching indefinitely. In this case it is the value -3.

The graph of the function is shown in the attached image.

The correct option is:

"Y-intercept of (0, −1), starts down on the left, gets closer to y = −3 on the right"