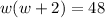Question

ohn has 48 square centimeter tiles he wants to use to create a mosaic. He wants the mosaic to be rectangular with a length that is 2 centimeters longer than the width. Which equation could John solve to find w, the greatest width in centimeters he can use for the mosaic? w(w – 2) = 48 w(w + 2) = 48 2w(w – 2) = 48 2w(w + 2) = 48

Answer 1

the answer is w(w+2).

Answer 2

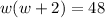`w(w+2)=48` can be used by John.

Explanation:

John has 48 square centimeter tiles he wants to use to create a mosaic.

We can say that 48 square cm is the area of the rectangle.

Let the width of the mosaic be = w

So, given is, He wants the mosaic to be rectangular with a length that is 2 centimeters longer than the width.

`l=w+2`

Now area of rectangle is given as =
`length* width`

`48=l* w`

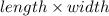
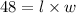
Substituting l= w+2

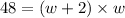`48=(w+2)* w` square cm

Hence, the equation John can use to solve and find w, the greatest width in centimeters he can use for the mosaic is :

`w(w+2)=48`