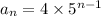Answer:
The explicit formula of the geometric sequence is:
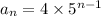
Explanation:
The explicit formula is the expression where the nth term is given in terms of the first term of the sequence.
We know that the explicit formula for a geometric sequence is given by:
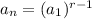
Here we are given:
The second and fifth terms as: 20 and 2500 respectively.
i.e.
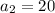 and
and
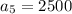
i.e.
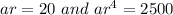
Hence,
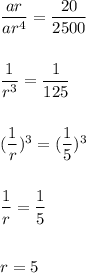
Also,
we have:
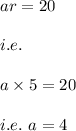
Hence, the explicit formula is given by: