Question

Use the arc length formula to find the length of the curve y = 5x − 4, −1 ≤ x ≤ 3. check your answer by noting that the curve is a line segment and calculating its length by the distance formula

Answer 1

The given curve is y = 5x -4, -1 ≤ x ≤ 3.

The length of the arc is computed from the formula

`S= \int_(-1)^(3) \,\sqrt{1+ ((dy)/(dx) )^(2)} \, dx`

The derivative is
y' = 5

Therefore

`S = \int_(-1)^(3) √(1+25) \, dx =√(26)*(3-(-1))=20.396`

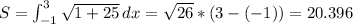
Note that
x = -1 +> y = 5(-1) - 4 = -9
x = 3 => y = 5(3) - 4 = 11
The distance between the points (-1, -9) and (3, 11) from the distance formula is
D = √[(3-(-1))² + (11-(-9))²] = √(16+400) = 20.396
This answer agrees with that obtained by integration.

Answer: 20.396
Obtained by integration and verified by the distance formula.