Question

He electric potential at a certain distance from a point charge can be represented by v. what is the value of the electric potential at twice the distance from the point charge?

Answer 1

Coulomb's Law for the electric field due to a point charge is

`E=k_(e) (q)/(r^(2))`
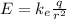
where
E = electric field, V

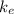
`k_(e)`= Coulom's constant, 8.98755 x 10²
q = point charge, C
r = distance from the pont charge, m

At distance, r, let the electric potential be

`v=k_(e) (q)/(r^(2))`

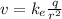
At twice the distance from q, the electric potential is

`v'=k_(e) (q)/((2r)^(2)) \\ = (1)/(4) k_(e) (q)/(r^(2)) \\ = \frac1x}{4}v`

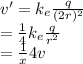
Answer:
At twice the distance from the charge, the electric decreases by a factor of 4.