Question

Suppose that we have the following sequence :

a_1=1
a_n=1/2 a_(n-1) , for n>1

We define a new sequence as such :
b_1=a_1
b_n=b_(n-1)+a_n

Find the 50th term of the sequence b_n.
Find the 1000000th term of the sequence b_n.

Answer 1

Given:
a₁ = 1

`a_(n) = (1)/(2) a_(n-1),\,n\ \textgreater \ 1`
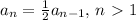
Therefore
a₂ = 1/2
a₃ = (1/2)*(1/2) = (1/2)²
...

`a_(n) = (1/2)^(n-1)`

Also,
b₁ = a₁

`b_(n) = b_(n-1)+a_(n)`
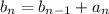
Therefore
b₁ = 1
b₂ = b₁ + a₂ = 1 + (1/2)
b₃ = b₂ + a₃ = 1 + 1/2 + (1/2)²
...

`b_(n) = 1 +\Sigma_(k=1)^(n-1) \,(1/2)^(k)`
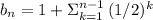
This is the sum of a geometric sequence with common ratio r=1/2.

The 50th term is

`b_(50) = 1 + ((1/2)[1-(1/2)^(49)])/(1-(1/2)) =2`

The 1000000th term is

`b_(1000000) = 1 + ((1/2)[1-(1/2)^(999999)])/(1-(1/2))=2`