Area of a triangle
The area of a triangle is found using its base and height:
In this case, if we rotate the given triangle, we have:
Then, we have:

We have to find the height in order to find the area of this triangle.
Sum of inner angles
Since the sum of the inner angles of a triangle is 180º, then:
∠V + ∠X + ∠W = 180º
↓ since ∠X=55º and ∠W=67º
∠V + 55º + 67º = 180º
∠V + 122º = 180º
Solving for ∠V:
∠V + 122º = 180º
↓ taking 122º to the right side of the equation
∠V = 180º - 122º = 58º
Then,
∠V = 58º
Height
Analyzing the triangle, we can see that drawing the height a right triangle is formed:
We have that:
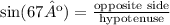
In this right triangle we have that:
height = opposite side
XW = hypotenuse
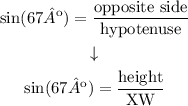
Then, we have an equation for the height:
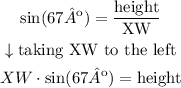
height = XW · sin(67º)
Then, if we find the length of the side XW, we will find the height.
XW measure
We have that, using the Sines Theorem (it relates the angles and their opposite side):

Then, we have an equation for XW:
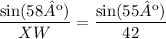
Solving the equation for XW, we have:
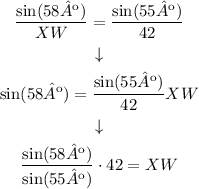
Solving the operation we have that:
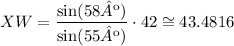
Then
XW ≅ 43.4816
Height PART 2
Now, we can find the height:
height = 43.4816 · sin(67º)
height = 43.57 · 0.92 ≅ 40.025
Now, we have the height:
height ≅ 40.025
We are going to use it to find the area:
Area PART 2

Now, we have the area:
area = 840.525 m²
If we round the area to the nearest tenth (one digit after the decimal point):
840.525 ≅ 840.5
Then,
area = 840.5 m²
Final answer: area = 840.5 m²