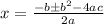Given:
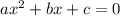
Required:
To derive the quadratic formula.
Step-by-step explanation:
Consider the given equation,
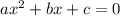
Divide all terms by a, we get
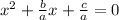
Subtract the constant term from both sides of the equation,
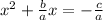
To have a square on the left side the third term (constant) should be
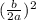
So add that amount to both sides
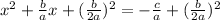
Re-write the left-side as a square.
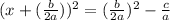
Take the square root of both sides, we get
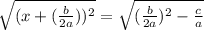
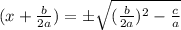
Now,
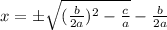
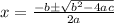
Final Answer:
The quadratic formula is