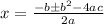Question

1. Derive the quadratic formula from ax^2 + bx + C = 0 by completing the square.

Answer 1

Given:

`ax^2+bx+c=0`

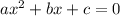
Required:

To derive the quadratic formula.

Step-by-step explanation:

Consider the given equation,

`ax^2+bx+c=0`

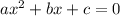
Divide all terms by a, we get

`x^2+(b)/(a)x+(c)/(a)=0`

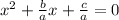
Subtract the constant term from both sides of the equation,

`x^2+(b)/(a)x=-(c)/(a)`

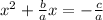
To have a square on the left side the third term (constant) should be

`((b)/(2a))^2`

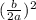
So add that amount to both sides

`x^2+(b)/(a)x+((b)/(2a))^2=-(c)/(a)+((b)/(2a))^2`

Re-write the left-side as a square.

`(x+((b)/(2a)))^2=((b)/(2a))^2-(c)/(a)`

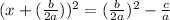
Take the square root of both sides, we get

`\sqrt{(x+((b)/(2a)))^2}=\sqrt{((b)/(2a))^2-(c)/(a)}`
`(x+(b)/(2a))=\pm\sqrt{((b)/(2a))^2-(c)/(a)}`

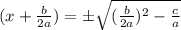
Now,

`x=\pm\sqrt{((b)/(2a))^2-(c)/(a)}-(b)/(2a)`
`x=(-b\pm√(b^2-4ac))/(2a)`

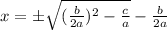
Final Answer:

The quadratic formula is

`x=(-b\pm b^(2)-4ac)/(2a)`