Question

An ellipse has vertices along the major axis at (0, 8) and (0, –2). The foci of the ellipse are located at (0, 7) and (0, –1). What are the values of a, b, h, and k, given the equation below? (y-k)^2/a^2+(x+h)^2/b^2=1

Answer 1

check the picture below, so it looks like so.

now hmm, from the provided vertices and focus point, you can pretty much see what "a" is, half of the major axis, is just 5.

now, the center is from either vertex to half-way up, or "a" units up, so say from -2 + 5, is at 3, so the center is at 0, 3.

now, the distance from a focus point to the center, is 4 units, like say from 0, 3 up to 0,7.


`\bf \textit{ellipse, vertical major axis}\\\\ \cfrac{(y-{{ h}})^2}{{{ a}}^2}+\cfrac{(x-{{ k}})^2}{{{ b}}^2}=1 \qquad \begin{cases} center\ ({{ h}},{{ k}})\\ vertices\ ({{ h}}, {{ k}}\pm a)\\ c=\textit{distance from}\\ \qquad \textit{center to foci}\\ \qquad \sqrt{{{ a }}^2-{{ b }}^2}\\ ----------\\ h=0\\ k=3\\ a=5\\c=4 \end{cases} \\\\\\ \cfrac{(y-3)^2}{5^2}+\cfrac{(x-0)^2}{b^2}=1`

now, let' s find "b".


`\bf c=√(a^2-b^2)\implies c^2=a^2-b^2\implies b^2=a^2-c^2 \\\\\\ b=√(a^2-c^2)\implies b=√(5^2-4^2)\implies b=3`

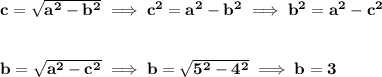
so, just plug that in.

Answer 2

a = 5

b = 3

h = 0

k = 3

Explanation:

just got it right on edg :)