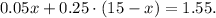Question

3. A purse contains $1.55 in nickels and quarters. If there are 15 coins,how many are nickels?How to make the equation for this problem ?

Answer 1

Step-by-step explanation

In this kind of exercise, the first step is to define variables (the things you want to find) tagging them by a letter:

x := # of nickels in the purse,

y := # of quarters in the purse.

The next step is to translate the relationship between the variables into equations. In this case, the expression: "There are 15 coins" means

`x+y=15.`

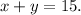
Besides, the expression: "... contains $1.55 in nickels and quarters" means

`0.05x+0.25y=1.55.`

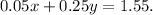
In summary, we have a 2x2 system of linear equations (don't worry about the name):

`\begin{cases}x+y=15 \\ 0.05x+0.25y=1.55\end{cases}`

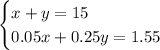
To solve it, we need to get rid of one variable. Let's eliminate y. Multiplying the second equation by -4, we get

`\begin{gathered} -4\cdot(0.05x+0.25y=1.55), \\ -4\cdot(0.05x)-4\cdot(0.25y)=-4\cdot1.55, \\ -0.2x-y=-6.2. \end{gathered}`

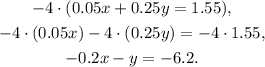
Adding the equation we just obtained with the first in the system, we get

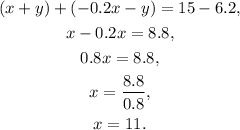
`\begin{gathered} (x+y)+(-0.2x-y)=15-6.2, \\ x-0.2x=8.8, \\ 0.8x=8.8, \\ x=(8.8)/(0.8), \\ x=11. \end{gathered}`Answer

The number of nickels in the purse is 11.

The single equation we need to solve the problem is

`0.05x+0.25\cdot(15-x)=1.55.`