There are a lot of steps involved in this, so pay attention. First step is to expand the squared quantity and FOIL it out, like this:
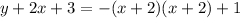
and
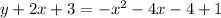
We are going to combine all the like terms now and get them all on one side of the equation:
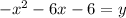
Now we are going to complete the square on the polynomial in order to find the vertex. Do this by first setting the equation equal to 0 and then moving the constant over to the other side of the equals sign, like this:
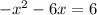
and now factor out the negative sign (cuz negative signs are a pain):
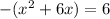
. To complete the square, you take half the linear term, square it, and add it in to both sides. Our linear term is 6x. Half of 6 is 3, and 3 squared is 9. That's easy to add in on the left side, but we cannot forget that fact that we factored out a negative 1, and that the negative 1 is still there and has to be taken into consideration when we "add" in a 9 to the other side. We actually multiply the negative 1 times the 9 and that's what's added in to the right:
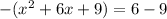
What you do when you complete the square is create a perfect square binomial on the left, which we have and which looks like this:
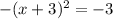
When we move the 3 back over to be with its mates (the 3 is the y coordinate for the vertex), we have the actual sign of the y coordinate. The number inside the parenthesis with the x is the x coordiante of the vertex in the form
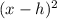
. So the vertex of your problem is (-3, 3). The negative outside the parenthesis just indicates to us that the parabola is an upside down one, like a mountain instead of a valley.