I think you're factoring this...? You can do that by grouping here. Put the 4 terms in groups of 2 and factor out the greatest common factor. What's left behind is a common binomial factor that can also then be factored out. Like this:
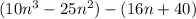
Factoring what we can out of both sets gives us this:
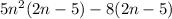
The 2n-5 is a common factor between both the sets of terms, which in turn can also be factored out:
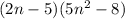
I'm not exactly sure what you are doing with this, but we can keep factoring for the sake of completeness. The 5 n-squared term can also be factored:
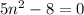
and
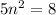
and
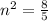
so
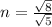
. Simplifying that down its simplest is this:

So your three factors for that polynomial are
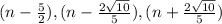
,