Question

Find the x-intercepts of the parabola with the vertex (4,-1) and y-intercpet (0,15). write your answer in this form, (x1,y1)(x2.y2)

use this method (y-k)=a(x-h)^2 to solve the problem

Answer 1

If you fit the vertex and the y-intercept into that form of the parabola, what you get is this:

`a(0-4) ^(2) =(15+1)` and

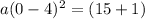
`a(-4) ^(2) =16` and 16a=16. Solve that a to get that a = 1. Now you have your true parabola equation in vertex form, which is:

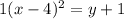
`1(x-4) ^(2) =y+1` or just

`(x-4) ^(2) =y+1`
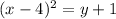
Follow my work here to find the x-intercepts:

`(x-4) ^(2) -1=y`
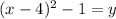
(x-4)(x-4)-1=y and
`x^(2) -8x+16-1=y`
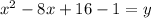
Simplifying by combining like terms gives you this parabola:

`x^(2) -8x+15=y`
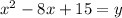
In order to find the x-intercepts, or the roots of the parabola as they are also known as, you have to set y equal to 0 (because the x-intercepts are found when y = 0, right?)

`x^(2) -8x+15=0`
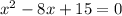
Factoring that gives you (x-5)(x-3)=0 and that x-5=0 and x-3=0. Solving each of those simple equations gives you x=5 and x=3 when y=0. So the roots, in the form you require them, are (5, 0) and (3, 0)