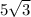Question

Suppose triangle ABC has vertices at A(1, 0), B(10, 0), and C(2, 6). After a 60° counterclockwise rotation about the origin, vertex B' has coordinates (5, ?).

Answer 1

check the picture attached.

Let OB be the radius of circle with center O.

Let B' be the image of B after the described rotation

OB and OB' are sides of the equilateral triangle OBB'.

The x coordinate of B' is the midpoint of OB, that is 5.

In the right triangle B', point (5, 0) and B:

Distance point (5, 0) to B is 5
|B'B|=|OB|=10

so by the pythagorean theorem:


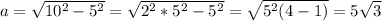
`a= \sqrt{ 10^(2) - 5^(2) } = \sqrt{ 2^(2) *5^(2) - 5^(2) }= \sqrt{5^(2)(4-1)}=5 √(3)` units



Answer:
`5 √(3)`