Question

Determine the number of possible triangles, ABC, that can be formed given B = 45°, b = 4, and c = 5.

Answer 1

2

Explanation:

this is right trust

Answer 2

Given:
m∠B = 45°
b = 4
c = 5

From the Law of Sines, obtain

`(sinC)/(c)= (sinB)/(b) \\ sinC=( (c)/(b))sinB \\sinC = ( (5)/(4) )sin(45^(o))=0.884\\ C = sin^(-1)0.884=62.1^(o)`
This yields
m∠A = 180 - 45 - 62.1 = 72.9°

`a=( (sinA)/(sinB))b=( (sin(72.9^(o)))/(sin(42^(o))))4=5.41`
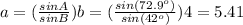
The first triangle has
∠A=72.9°, m∠B=45°, m∠C = 62.1°, a=5.41, b=4, c=5.

Also,

`m\angle{C} = sin^(-1)0.884 = 117.9^(o)`
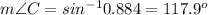
This yields
m∠A = 180 - 45 - 117.9 = 17.1°

`a=( (sinA)/(sin(45^(o))) )4=1.66`
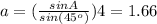
The second triangle has
m∠A = 17.1°, m∠B = 45°, m∠C = 117.9°, a = 1.66, b = 4, c = 5

Answer: There are 2 possible triangles.