Question

The following graph describes function 1, and the equation below it describes function 2:

Function 1

graph of function f of x equals negative x squared plus 8 multiplied by x minus 15

Function 2

f(x) = −x2 + 2x − 15

Function ____ has the larger maximum.
(Put 1 or 2 in the blank space)

Answer 1

The Function __1__ has the larger maximum.

Explanation:

The given functions are

Function 1:

`f(x)=-x^2+8x-15`

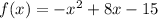
Function 2:

`f(x)=-x^2+2x-15`

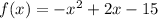
Both functions are downward parabola because the leading coefficient is negative. So, the vertex is the point of maxima.

If a function is
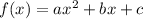`f(x)=ax^2+bx+c`, then its vertex is

`Vertex=((-b)/(2a), f((-b)/(2a)))`

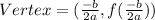
The vertex of Function 1 is

`Vertex=((-8)/(2(-1)), f((-8)/(2(-1))))`

`Vertex=(4, f(4))`

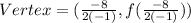
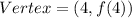
The value of f(4) is

`f(4)=-(4)^2+8(4)-15=1`

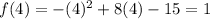
The vertex of Function 1 is (4,1). Therefore the maximum value of Function 1 is 1.

The vertex of Function 2 is

`Vertex=((-2)/(2(-1)), f((-2)/(2(-1))))`

`Vertex=(1, f(1))`

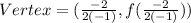
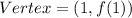
The value of f(1)is

`f(1)=-(1)^2+2(1)-15=-14`

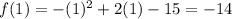
The vertex of Function 2 is (1,-14). Therefore the maximum value of Function 2 is -14.

Since 1>-14, therefore Function __1__ has the larger maximum.

Answer 2

Function 1 ⇒
`f(x)=- x^(2) +8x-15`
Function 2 ⇒
`- x^(2) +2x-15`

Both functions are shown in the graph below

As well as graphing, we can also find out the function with the highest maximum by using the formula to find the x-coordinate when the function is maximum/minimum


`x=- (b)/(2a)`

Maximum vertex for function 1 is
`x=- (8)/((2)(-1)) = (-8)/(-2) =4`
Maximum vertex for function 2 is
`x=- (2)/((-2)(-1))= (-2)/(-2)=1`

Hence the function with the highest maximum is function 1