Question

one zero is given find all others P of x equals x to the third power minus 4x squared minus 25 x + 100 ; -5

Answer 1

The expression is:

`x^3-4x^2-25x+100`

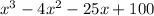
We know that one of the zeros of this expression is x=-5. We have to find the others.

Then, we can write this expression as:

`\begin{gathered} x^3-4x^2-25x+100=(x+5)(ax^2+bx+c) \\ ax^2+bx+c=(x^3-4x^2-25x+100)/(x+5) \end{gathered}`

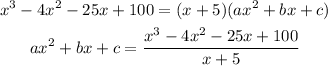
We have to perform the polynomial division:

`\begin{gathered} (x^3-4x^2-25x+100)/(x+5)=(x^3-4x^2-25x+100-5x^2+5x^2)/(x+5) \\ ((x^3+5x^2)-4x^2-25x+100+5x^2)/(x+5) \\ (x^2(x+5))/(x+5)+(-4x^2-25x+100-5x^2)/(x+5) \\ x^2+(-9x^2-25x+100)/(x+5) \\ x^2+(-9x^2-25x+100+45x-45x)/(x+5) \\ x^2+((-9x^2-45x)/(x+5)+(-25x+45x+100)/(x+5)) \\ x^2-9x+(20x+100)/(x+5) \\ x^2-9x+20 \end{gathered}`
`x^3-4x^2-25x+100=(x+5)(x^2-9x+20)`

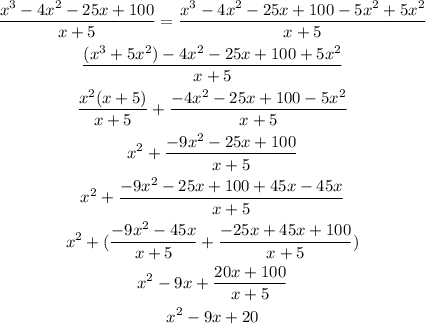
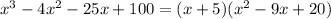
Now, we can calculate the zeros of the quadratic polynomial as:

`\begin{gathered} x=\frac{-(-9)\pm\sqrt[]{(-9)^2-4\cdot1\cdot(20)}}{2\cdot1} \\ x=\frac{9\pm\sqrt[]{81-80}}{2} \\ x=\frac{9\pm\sqrt[]{1}}{2} \\ x_1=(9-1)/(2)=(8)/(2)=4 \\ x_2=(9+1)/(2)=(10)/(2)=5 \end{gathered}`

Answer: the other two zeros are x=4 and x=5