Question

The population of a local species of beetle can be found using an infinite geometric series a1=960 and the common ratio is .25 write the sum in sigma notation and calculate the sum of possible that will be the upper limit of this population

Sigma 960 (1/4)^i-1 ; the sum is 1280
Signa 960 (1/4)^-1 the sun is divergent
Sigma 960 (1/4)^i sum is 1280
Sigma (1/4)^i sum is divergent

I=1 for them all

Answer 1

Sigma 960(1/4)^(i-1)

Since r^2<1, the sum is convergent and has a value of

960/(1-1/4)

960/(3/4)

4(960)/3

1280

Answer 2

The answer is:

Sigma 960 (1/4)^i-1 ; the sum is 1280

Explanation:

We are given the first term of the geometric sequence as:

`a_1=960`

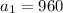
Also, the common ratio of the terms in geometric sequence is:
`(1)/(4)`

We know that if the series is a geometric series than the sum of the terms is given by:

`a+ar+ar^2+.....\\\\=a(1+r+r^2+....)\\\\=\sum ar^(n-1)`

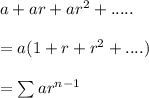
where a is the first term of the series and r is the common difference.

Here a=960

and r=1/4

Hence,

The sum of the series is:

`=\sum 960((1)/(4))^(i-1)`

Now we know that the sum of the infinite geometric series is given by:

`S=(a)/(1-r)`

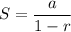
where S is the sum of the series.

Hence, here the sum of the series is calculated by:

`S=(960)/(1-(1)/(4))\\\\\\S=(960)/((3)/(4))\\\\\\S=(960* 4)/(3)\\\\\\S=1280`

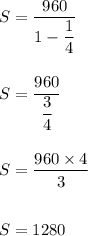
Hence, the sum is: 1280