Question

Which graph correctly represents
x + 2y ≤ 4?

Answer 1

x + 2y < = 4
2y < = -x + 4
y < = -1/2x + 2

u will have a solid line (because there is an = sign in the problem)....the slope will be -1/2...so ur line is going down....u have a y int (where ur line crosses the y axis at (0,2).....u have an x int (where ur line crosses the x axis at (0,4)..ur line will be shaded below the line.

Answer 2

Step-by-step explanation:

`x + 2y \leq 4`

To graph this inequality we replace <= symbol with = sign

`x + 2y =4`

subtract x on both sides

`2y =-x+4`

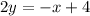
divide both sides by 2

`y= (-1)/(2) x +2`

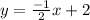
Graph the equation using a table

LEts assume some number for x and find out y

x
`y= (-1)/(2) x +2`

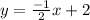
-2 3

0 2

2 1

Now graph the equation using points (-2,3) (0,2)(2,1)

use solid line for graphing

Now use test point (0,0) for shading

`x + 2y \leq 4`

`0 + 2(0) \leq 4`

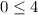`0 \leq 4` true

So we shade the region that contains (0,0)

the graph is attached below