Question

F the radius of a sphere is increasing at the constant rate of 2 cm/min, find the rate of change of its surface area when the radius is 100 cm

Answer 1

The surface area of a sphere of radius r is
A(r) = 4πr²

The rate of change of the surface area with respect to time is

`(dA)/(dt) = (dA)/(dr) (dr)/(dt)`

The radius increases at the constant rate of 2 cm/min, therefore

`(dA)/(dt) = 2 (dA)/(dr)=2*(8 \pi r) =16 \pi r`

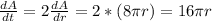
When r = 100 cm, the rate of change of the surface area is
16π(100) cm²/min
= 1600π cm²/min
= 5026.5 cm²/min

Answer: 1600π or 5026.5 cm²/min