Using Pythagorean inequalities, determine which set of the given three sides produces an obtuse triangle. A. 4, 5, 6 B. 5, 13, 19 C. 12, 14, 25 D. 21, 72, 75

Question

asked Mar 25, 2018 15.6k views

2 Answers

Amartine · Answer 1 · 2018-03-31T01:01:38+0000

Answer:

Obtuse triangle sets

B. 5, 13, 19

C. 12, 14, 25

Explanation:

The Pythagorean inequality for the sides of the triangle to be an obtuse:

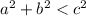a^2 + b^2 < c^2 , where a, b and c are the sides of the triangle.

The other Pythagorean inequalities are:

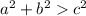a^2 + b^2 > c^2 , for Acute triangle

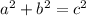a^2 + b^2 = c^2 , for Right triangle

Now let's check which set of the given sets satisfy the above inequality.

Option A

4, 5, 6

Here a = 4, b = 5 and c = 6

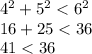
$4^2 + 5^2 < 6^2\\16 + 25 < 36\\41 < 36\\$

Which is not true.

Here
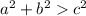, So this is Acute triangle

Option B

5, 13, 19

Here a = 5, b = 13 and c = 19

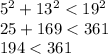
$5^2 + 13^2 < 19^2\\25 + 169 < 361\\194 < 361\\$

Which is true. This is Obtuse triangle

Option C

Here a = 12, b = 14 and c = 25

$12^2 + 14^2 < 25^2\\144 + 196 < 625\\340 < 625\\$

Which is true. This is obtuse triangle.

Option D

Here a = 21, b = 72 and c = 75

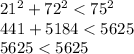
$21^2 + 72^2 < 75^2\\441 + 5184 < 5625\\5625 < 5625\\$

Which is not true for obtuse.

Here
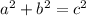, for Right triangle

So this is Right triangle.