Question

Based on the table, which statement best describes a prediction for the end behavior of the graph of f(x)? As x → ∞, f(x) → –∞, and as x → –∞, f(x) → ∞ As x → ∞, f(x) → ∞, and as x → –∞, f(x) → ∞ As x → ∞, f(x) → ∞, and as x → –∞, f(x) → –∞ As x → ∞, f(x) → –∞, and as x → –∞, f(x) → –∞

Answer 1

The end behavior of the graph of the function f(x) is:

f(x) → ∞, and as x → –∞, f(x) → ∞ As x → ∞,

Step-by-step explanation:

Based on the table we could observe that the function f(x) is increasing to the left of -1 as well to the right of -1 and it attains the minimum value to be -6.

Hence, it can be predicted that the end behavior of the graph of the function f(x) goes to infinity in the left and also it goes to infinity in the right.

Hence, the statement that best describes the end behavior of the graph of f(x) is:

f(x) → ∞, and as x → –∞, f(x) → ∞ As x → ∞.

Answer 2

Answer: The correct option is B, i.e., "As x → ∞, f(x) → ∞, and as x → –∞, f(x) → ∞".

Step-by-step explanation:

From the table it is noticed that the first row represents the value of x and the second row represents the value of f(x).

The value of f(x) is 14 at x = -5, after that the value of f(x) is decreased as the value of x increases.

The value of f(x) remains unchanged when the value of x approaches to 0 from 1.

The value of f(x) is -6 at x = 0, after that the value of f(x) is increased as the value of x increases.

From the table it is noticed that as the value of x approaches to positive infinity the value of f(x) is also approaches to positive infinity.

`f(x)\rightarrow\infty \text{ as }x\rightarrow\infty`

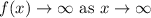
From the table it is noticed that as the value of x approaches negative infinity the value of f(x) is also approaches to positive infinity.

`f(x)\rightarrow\infty \text{ as }x\rightarrow-\infty`

These statement are shown in second option, therefore the second option is correct.