Question

Can the polynomial below be factored into a perfect square? If not, select the answer that best describes why not.

64x^2+49x+8
A.

The x^2 coefficient does not permit the factoring.


B.

The x^2 coefficient does permit the factoring, but the x coefficient does not permit the factoring.


C.

The constant value does not permit the factoring.


D.

The polynomial may be factored into a perfect square.

Answer 1

Option B;
A suitable x-coefficient for a quadratic function that factors into a perfect square has to be even.

Answer 2

Option B is correct.

Explanation:

We will work with the formula :
`(a+b)^(2)`

=
`a^(2)+2ab+b^(2)`

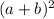
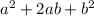
Given polynomial is :

`64x^(2) +49x+8`

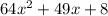
here a =
`\sqrt{64x^(2) } =8x`

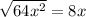
b =
`√(8)= 2√(2)`

2ab =
`2*8x*2√(2) =32√(2)x`

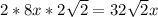
Now, we can see that the middle term should be
`32√(2) x` but in the question, it is given 49x

So, option B is true that - The x^2 coefficient does permit the factoring, but the x coefficient does not permit the factoring.