Question

Which of the following would best represent a cosine function with an amplitude of 3, a period of pi/2 , and a midline at y = –4? (1 point)

f(x) = –4 cos 4x + 3

f(x) = 3 cos(x – pi/2 ) – 4

f(x) = 4 cos(x – pi/2 ) + 3

f(x) = 3 cos 4x – 4

Answer 1

D) f(x) 3 cos 4x-4 (I just took it)

Answer 2

To transform the function
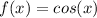
`f(x)= cos(x)` to have the amplitude of 3, we need to multiply the constant 3 to the function f(x), so we have
`y=3f(x)`

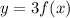
To transform the function
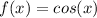
`f(x)=cos(x)` to have the midline
`y=-4` we need to subtract
`f(x)` by 4, so we have
`y=f(x)-4`,

To transform the function
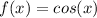
`f(x)=cos(x)` to have period of
`( \pi )/(2)`, we need to divide the original period
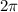
`2 \pi` by 4, so we have
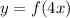
`y=f(4x)`. Note that it is the
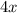
`4x` gives the effect of dividing the points on x-axes by 4 and the period is read on x-axes

Hence, the full transformation is given
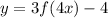
`y=3f(4x)-4` which is the last option