Question

A square garden plot has an area of 75 ft2. a. Find the length of each side in simplest radical form. b. Calculate the length of each side to the nearest tenth of a foot.

Answer 1

A square garden plot has an area of 75 ft2.
a. Find the length of each side in simplest radical form.
First, a square area (A) = length (l)^2
A(ft2) = l^2 --> so l(ft) = square root (sr) of A
l = srA = sr75
Next, factor out 75 into number with even roots: 25•3 = 75
So l = sr25•sr3 --> l = 5•sr3 ft
5•sr3 is in the simplest radical form

b. Calculate the length of each side to the nearest tenth of a foot.
l = sr3 = 1.732 --> so 5•1.732 = 8.66ft
Tenth is one place to the right of the decimal, so l = 8.7 ft

Answer 2

a)the length of each side is
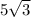`5\sqrt3` feet

b)In the nearest tenth the length of the side is 8.7 feet.

Explanation:

The area of the square garden is 75 square feet.

a) Let x be the length of each side.

We know that,

`\text{Area of square}=\text{(Side)}^2`

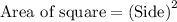
Hence, we have

`75=x^2\\\\x=√(75)\\\\x=5√(3)`

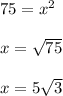
Thus, the length of each side is
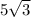`5\sqrt3` feet

b)

In the nearest tenth the length of the side is 8.7 feet.