Question

The average annual salary of the employees of a company in the year 2005 was $80,000. It increased by the same factor each year and in 2006, the average annual salary was $88,000. Let f(x) represent the average annual salary, in thousand dollars, after x years since 2005. Which of the following best represents the relationship between x and f(x)?

f(x) = 88(0.88)x
f(x) = 88(1.1)x
f(x) = 80(0.88)x
f(x) = 80(1.1)x

Answer 1

the answer is f(x)=80(1.1)x

Answer 2

Answer:
`f(x) = 80 ( 1.1 ) ^x`

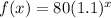
Explanation:

Let the function that shows the average annual salary after x years since 2005 is,

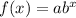`f(x) = ab^x` ----- (1)

Where a and b are any unknown numbers.

For x = 0,

`f(0) = ab^0= a`

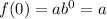
But According to the question,

The average annual salary of the employees of a company in the year 2005 was $80,000.

Therefore, f(0)=80000 dollars.

⇒ a = 80000

From equation (1),

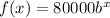`f(x) = 80000 b^x` ------- (2)

Now again according to the question,

In 2006, the average annual salary was $88,000

But the average annual salary in 2006 is
`f(1) = 80000 b^1`

⇒
`80000 b^1=88000`

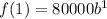
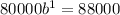
⇒ b = 1.1

Putting the value of b in equation (2),

The average annual salary after x years since 2005 is,

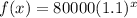`f(x) = 80000 (1.1)^x` dollars

Or
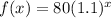`f(x) = 80 (1.1)^x` thousand dollars

Thus, Fourth Option is correct.