Question

Adult male heights are normally distributed with a mean of 70 inches and a standard deviation of 3 inches. The average basketball player is 79 inches tall. Approximately what percent of the adult male population is taller than the average basketball player? 0.135% 0.875% 49.875% 99.875%

Answer 1

z = (x - mean) / SD = (79 - 70) / 3 = 3
P (Z > 3)? = 1 - F (z) = 1 - F (3) = 0.00135

Answer 2

A. 0.135%

Explanation:

We have been given that adult male heights are normally distributed with a mean of 70 inches and a standard deviation of 3 inches. The average basketball player is 79 inches tall.

We need to find the area of normal curve above the raw score 79.

First of all let us find the z-score corresponding to our given raw score.

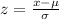`z=(x-\mu)/(\sigma)`, where,

`z=\text{z-score}`,

`x=\text{Raw-score}`,

`\mu=\text{Mean}`,

`\sigma=\text{Standard deviation}`.

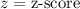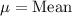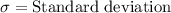Upon substituting our given values in z-score formula we will get,

`z=(79-70)/(3)`

`z=(9)/(3)`

`z=3`

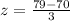
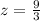
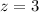
Now we will find the P(z>3) using formula:

`P(z>a)=1-P(z<a)`

`P(z>3)=1-P(z<3)`

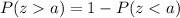
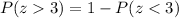
Using normal distribution table we will get,

`P(z>3)=1-0.99865`

`P(z>3)=0.00135`

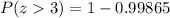
Let us convert our answer into percentage by multiplying 0.00135 by 100.

`0.00135* 100=0.135%`

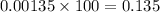
Therefore, approximately 0.135% of the adult male population is taller than the average basketball player and option A is the correct choice.