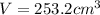Question

A cone-shaped hole is drilled into a solid cube of metal as shown. If the cube has sides of length 7 cm, what is the volume of the metal after the hole is drilled? Let π ≈ 3.14 and round your answer to the nearest tenth.

Answer 1

This problem really should have the image attached, as we are not quite sure what the radius of the cone is, nor are we sure about how deeply the cone-shaped hole is bored into the cube. When I did this, I just assumed that the radius of the cone was half the length of the cube which is 3.5, and I assumed that the height of the cone was the same as the height of the cube which is 7. So the volume for the cube itself is 7*7*7=343. Now we have to subtract from that the volume of the cube, which has a formula of
`V= (1)/(3) \pi r^(2) h`
If we fill in those values I'm assuming to be accurate, our formula then looks like this:

`V= (1)/(3)(3.14)( 3.5^(2) )(7)`
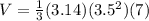
which equals 89.752 If we subtract the volume of the cone from the volume of the cube, we will get that volume of what's left is
`V=253.2 cm^(3)`