Question

Cylindrical coordinates? Hi,

I am having problems with a homework question,
I am asked to sketch the solid by the given inequalities.
0 <= theta <= pi/2 and r <= z <= 2
How do I find r?
If possible please guide me to the answer instead of giving it to me. I need to know this stuff.
Thanks in advance for any help.

Answer 1

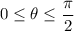
`0\le\theta\le\frac\pi2` tells you that
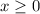
`x\ge0` and
`y\ge0`.

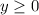
Recalling that in cylindrical coordinates,
`r^2=x^2+y^2\implies r=√(x^2+y^2)`, we then know that
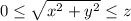
`0\le√(x^2+y^2)\le z`, and so we're confined to the first octant (where each of
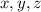
`x,y,z` are non-negative).

The upper limit of
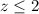
`z\le2` tells us that the region is bounded above by the plane
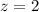
`z=2`, which is parallel to the
`x`-
`y` plane.

Meanwhile, the lower limit of
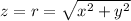
`z=r=√(x^2+y^2)` can be visualized by first squaring both sides:


`z=√(x^2+y^2)\implies z^2=x^2+y^2`

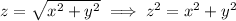
If you're not already familiar with what this equation represents, we can approach it piecemeal. At one extreme, when
`x=y=0`, we have
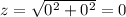
`z=√(0^2+0^2)=0`, so the region has a "vertex" at the origin.

When
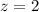
`z=2`, we have the Cartesian equation
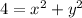
`4=x^2+y^2`, which corresponds to a circle of radius 2. Similarly, if we consider values of
`z` between 0 and 2, we end up with circles of increasing radii. Stacking these circles onto one another, we get a cone.

More specifically, the region is the part of the cone between the
`x`-
`y` plane and the plane
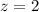
`z=2` restricted to the first octant.

(Image of region attached)