Question

True or false the center of the circumscribed circle about a triangle is equidistant to the vertices of the inscribed triangle

Answer 1

The answer is TRUE!!!!!

Answer 2

True

Explanation:

Consider triangle ABC inscribed in the circle with center at point O. Point O is a point of intersection of perpendicular bisectors of sides AC, AB and BC. According to the attached diagram, points E, F and G are midpoints of sides BC, AC and AB, respectively.

Then

• EB=EC;
• FC=FA;
• GA=GB.

Since segments OE, OF and OG are perpendicular bisectors of sides BC, AC and AB, then

• m∠OBE=m∠OCE=90°;
• m∠OCF=m∠OAF=90°;
• m∠OBG=m∠OAG=90°.

You get three pairs of congruent triangles:

1. ΔOBE≅ΔOCE;
2. ΔOCF≅ΔOAF;
3. ΔOBG≅ΔOAG.

This gives you that

`OB=OC=OA.`

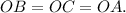
Each of these segments is a radius of the circumscribed circle about a triangle ABC, then the center of the circumscribed circle about a triangle is equidistant to the vertices of the inscribed triangle.