Question

If the directrix of a parabola is the horizontal line y = 3, what is true of the parabola?

a)The focus is at (0, 3), and the equation for the parabola is y2 = 12x.
b)The focus is at (0, –3), and the equation for the parabola is x2 = –12y.
c)The focus is at (3, 0), and the equation for the parabola is x2 = 12y.
d)The focus is at (–3, 0), and the equation for the parabola is y2 = –12x.

Answer 1

Answer: on e2020 it’s b

Step-by-step explanation:

Answer 2

The correct answer is b), or x² = -12y.

Step-by-step explanation:
This equation may be written in standard form as

`y=- (1)/(12) x^(2)`
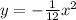
The coefficient in front of x² is negative so the curve is downward.
The vertex has coordinates (0,0).
The vertex is equidistant from the directrix and the focus, so the focus is (0, -3).