Question

William invested $6000 in an account that earns 5.5% interest, compounded annually. The formula for compound interest is A(t) = P(1 + i)t.

How much did William have in the account after 6 years? (APEX)

Answer 1

`\bf \qquad \textit{Compound Interest Earned Amount} \\\\ A=P\left(1+r\right)^(t) \quad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\to &\$6000\\ r=rate\to 5.5\%\to (5.5)/(100)\to &0.055\\ t=years\to &6 \end{cases} \\\\\\ A=6000(1+0.055)^6\implies A=(1.055)^6`

Answer 2

William have $8273.057 in the account after 6 years.

Explanation:

The given formula is
`A(t)=P(1+i)^t`

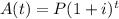
We have,

P = $6000

r = 5.5% = 0.055

t = 6

A =?

Substituting these values in the above formula to find A

`A(t)=6000(1+0.055)^6\\\\A(t)=8273.057`

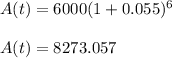
Therefore, William have $8273.057 in the account after 6 years.