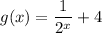Question

The graph shows f(x) = 1/2 and its translation, g(x).

Which describes the translation of f(x) to g(x)?

Answer 1

The translation function g(x) is given as:

`g(x)=(1)/(2^x)+4`

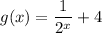
Explanation:

The parent function is f(x) and its representation is given as:

`f(x)=(1)/(2^x)`

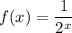
Now the graph g*x) is obtained by translation of the graph f(x) by some units.

Now as the graph of g(x) is a shift of the graph f(x) or the graph g(x) is translated by 4 units upwards.

hence the function g(x) is represented by:

g(x)=f(x)+4.

Hence the translation function g(x) is given as:

`g(x)=(1)/(2^x)+4`

Answer 2

As you can see, each point on f(x) is moved up 4 units to get to g(x), so the function is g(x) = f(x) + 4. The f(x) function cannot possibly be f(x)=1/2, though, because that would be a horizontal line through y = 1/2 and that function is clearly not a horizontal line. So whatever f(x) is REALLY, add 4 to the tail end of it to show its translation.